Chemical Heuristics in the 21st Century
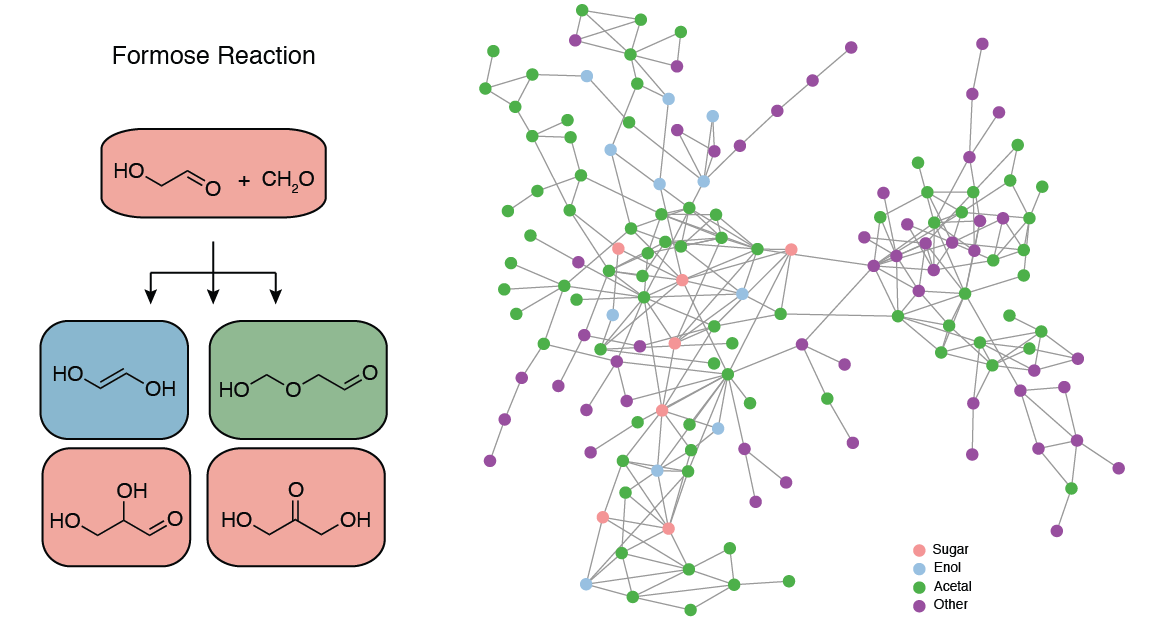
Networked Chemistry
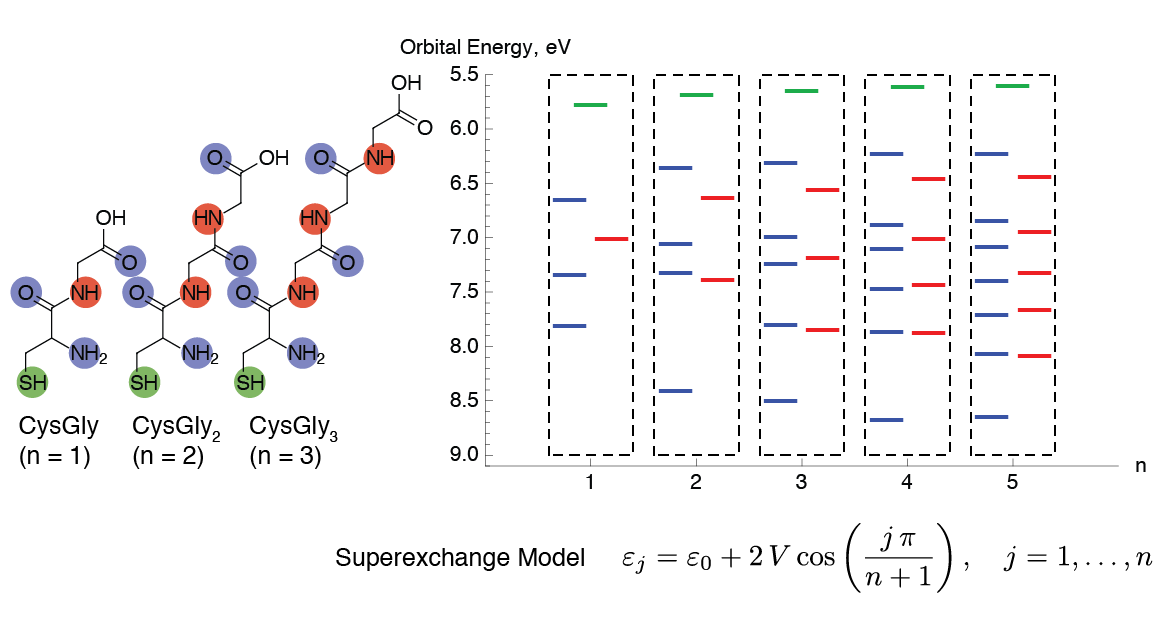
Conducting Molecules
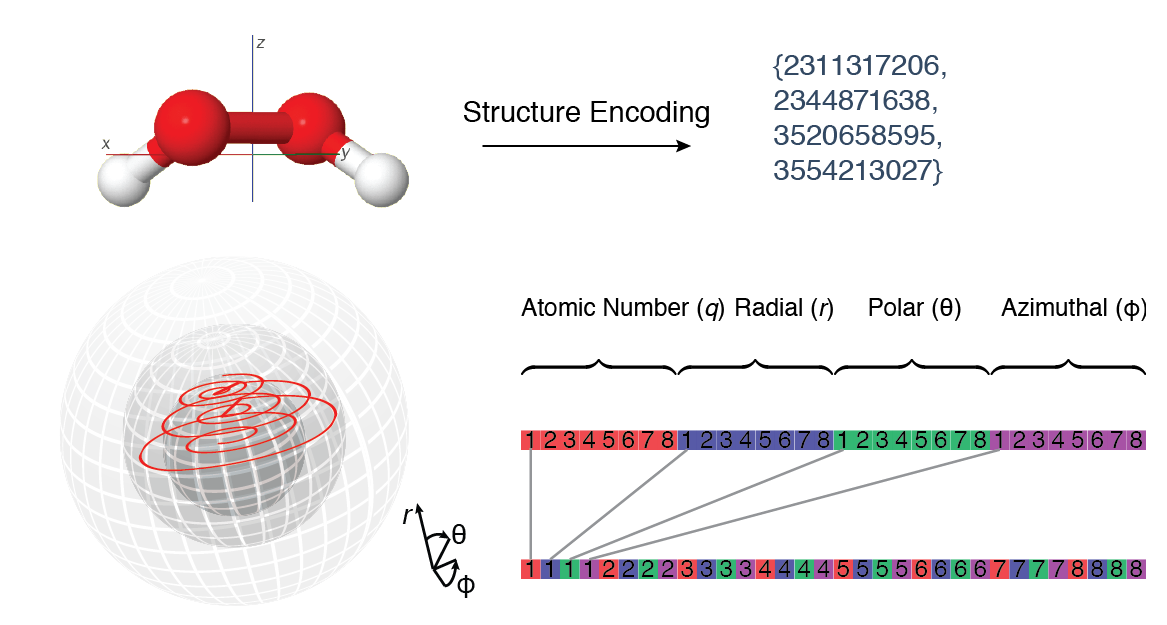
Encoding 3D Molecular Structure
Journals and Book Chapters
- Rappoport, D.; Furche, F. Photoinduced intramolecular charge transfer in 4-(dimethyl)-aminobenzonitrile—A theoretical perspective. J. Am. Chem. Soc. , 126, 1277–1284.
- Bark, T.; Zelewsky, von, A.; Rappoport, D.; Neuburger, M.; Schaffner, S.; Lacour, J.; Jodry, J. Synthesis and stereochemical properties of chiral square complexes of iron(II). Chem. Eur. J. , 10, 4839–4845.
- Rappoport, D.; Furche, F. Analytical time-dependent density functional derivative methods within the RI–J approximation, an approach to excited states of large molecules. J. Chem. Phys. , 122, 064105.
- Furche, F.; Rappoport, D. Density functional methods for excited states: Equilibrium structure and electronic spectra. In Computational Photochemistry; Olivucci, M., Ed.; Elsevier: Amsterdam, , pp. 93-128.
- Rappoport, D.; Furche, F. Excited States and Photochemistry. In Time-Dependent Density Functional Theory; Marques, M. A. L.; Ullrich, C. A.; Nogueira, F.; Rubio, A.; Burke, K.; Gross, E. K. U., Eds.; Springer: Berlin, Heidelberg, , pp. 337–354.
- Rappoport, D.; Furche, F. Lagrangian approach to molecular vibrational Raman intensities using time-dependent hybrid density functional theory. J. Chem. Phys. , 126, 201104.
- Chow, H. S.; Constable, E. C.; Frantz, R.; Housecroft, C. E.; Lacour, J.; Neuburger, M.; Rappoport, D.; Schaffner, S. Conformationally-locked metallomacrocycles—Prototypes for a novel type of axial chirality. New J. Chem. , 33, 376–385.
- Rappoport, D., Furche, F. Structure of Endohedral Fullerene Eu@C74. Phys. Chem. Chem. Phys. , 11, 6353–6358.
- Rappoport, D.; Crawford, N. R. M.; Furche, F.; Burke, K. Approximate Density Functionals: Which Should I Choose? In Encyclopedia of Inorganic Chemistry. Computational Inorganic and Bioinorganic Chemistry; Solomon, E. I.; King, R. B.; Scott, R. A., Eds.; Wiley: Chichester, , pp. 159–172.
- Saikin, S. K.; Olivares-Amaya, R.; Rappoport, D.; Stopa, M.; Aspuru-Guzik, A. On the chemical bonding effects in the Raman response: Benzenethiol adsorbed on silver clusters. Phys. Chem. Chem. Phys. , 11, 9401–9411.
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. , 133, 134105.
- Saikin, S. K.; Chu, Y.; Rappoport, D.; Crozier, K. B.; Aspuru-Guzik, A. Separation of Electromagnetic and Chemical Contributions to Surface-Enhanced Raman Spectra on Nanoengineered Plasmonic Substrates. J. Phys. Chem. Lett. , 1, 2740–2746.
- Rappoport, D.; Shim, S.; Aspuru-Guzik, A. Simplified Sum-Over-States Approach for Predicting Resonance Raman Spectra. Application to Nucleic Acid Bases. J. Phys. Chem. Lett. , 2, 1254–1260.
- Parkhill, J. A.; Rappoport, D.; Aspuru-Guzik, A. Modeling Coherent Anti-Stokes Raman Scattering with Time-Dependent Density Functional Theory: Vacuum and Surface Enhancement. J. Phys. Chem. Lett. , 2, 1849–1854.
- Rappoport, D. Basis-set quality and basis-set bias in molecular property calculations. ChemPhysChem, , 12, 3404–3413.
- Watson, M. A.; Rappoport, D.; Lee, E. M. Y.; Olivares-Amaya, R.; Aspuru-Guzik, A. Electronic structure calculations in arbitrary electrostatic environments. J. Chem. Phys. , 136, 024101.
- Rappoport, D.; Hutter, J. Excited-State Properties and Dynamics. In Fundamentals of Time-Dependent Density Functional Theory; Marques, M. A. L.; Maitra, N. T.; Nogueira, F. M. S.; Gross, E. K. U.; Rubio, A., Eds.; Springer: Berlin Heidelberg, , pp. 317–336.
- Olivares-Amaya, R.; Rappoport, D.; Munoz, P. A.; Peng, P.; Mazur, E.; Aspuru-Guzik, A. Can Mixed-Metal Surfaces Provide an Additional Enhancement to SERS? J. Phys. Chem. C, , 116, 15568–15575.
- Widom, J. R.; Rappoport, D.; Perdomo-Ortiz, A.; Thomsen, H.; Johnson, N. P.; Hippel, von, P. H.; Aspuru-Guzik, A.; Marcus, A. H. Electronic transition moments of 6-methyl isoxanthopterin—A fluorescent analogue of the nucleic acid base guanine. Nucleic Acids Res., , 41, 995–1004.
- Widom, J. R.; Lee, W.; Perdomo-Ortiz, A.; Rappoport, D.; Molinski, T. F.; Aspuru-Guzik, A.; Marcus, A. H. Temperature-dependent conformations of a membrane supported zinc porphyrin tweezer by 2D fluorescence spectroscopy. J. Phys. Chem. A, , 117, 6171–6184.
- Lockett, M. R.; Lange, H.; Breiten, B.; Héroux, A.; Sherman, W.; Rappoport, D.; Yau, P. O.; Snyder, P. W.; Whitesides, G. M. The binding of benzoarylsulfonamide ligands to human carbonic anhydrase is insensitive to formal fluorination of the ligand. Angew. Chem. Int. Ed., , 52, 7714–7717.
- Rappoport, D.; Galvin, C. J.; Zubarev, D. Yu.; Aspuru-Guzik, A. Complex chemical reaction networks from heuristics-aided quantum chemistry. J. Chem. Theory Comput., , 10, 897–907.
- Bowers, C. M.; Liao, K.-C.; Yoon, H. J.; Rappoport, D.; Baghbanzadeh, M.; Simeone, F. C; Whitesides, G. M. Introducing ionic and/or hydrogen bonds into the SAM//Ga2O3 top-interface of AgTS/S(CH2)nT//Ga2O3/EGaIn junctions. Nano Lett., , 14, 3521–3526.
- Cabalo, J. B.; Saikin, S. K.; Emmons, E. D.; Rappoport, D; Aspuru-Guzik, A. A state-by-state investigation of destructive interference in resonance Raman spectra of neutral tyrosine and tyrosinate anion with the simplified sum-over-states approach. J. Phys. Chem. A, , 118, 9675–9686.
- Jinich, A.; Rappoport, D.; Dunn, I.; Sanchez-Lengeling, B.; Olivares-Amaya, R.; Noor, E.; Bar Even; A.; Aspuru-Guzik, A. Quantum chemical approach to estimating the thermodynamics of metabolic reactions. Sci. Rep., , 4, 7022.
- Hellweg, A.; Rappoport, D. Development of new auxiliary basis functions of the Karlsruhe segmented contracted basis sets including diffuse basis functions (def2-SVPD, def2-TZVPPD, and def2-QVPPD) for RI-MP2 and RI-CC calculations. Phys. Chem. Chem. Phys, , 17, 1010–1017.
- Bowers, C. M.; Liao, K.-C.; Żaba, T.; Rappoport, D.; Breiten, B.; Baghbanzadeh, M.; Krzykawska, A.; Cyganik, P.; Whitesides, G. M. Characterizing the metal–SAM interface in tunneling junctions. ACS Nano, , 9, 1471–1477.
- Zubarev, D. Yu.; Rappoport, D.; Aspuru-Guzik, A. Uncertainty of prebiotic scenarios: The case of the non-enzymatic reverse tricarboxylic acid cycle. Sci. Rep., , 5, 8009.
- Baghbanzadeh, M.; Bowers, C. M.; Rappoport, D.; Żaba, T.; Gonidec, M.; Al-Sayah, M. H.; Cyganik, P.; Whitesides, G. M. Charge tunneling along short oligoglycine chains. Angew. Chem. Int. Ed., , 54, 14743–14747.
- Bowers, C. M.; Rappoport, D.; Baghbanzadeh, M.; Simeone, F. C.; Liao, K.-C.; Semenov, S. N.; Żaba, T.; Cyganik, P.; Aspuru-Guzik, A.; Whitesides, G. M. Tunneling across SAMs containing oligophenyl groups. J. Phys. Chem. C, , 120, 11331–11337.
- Markovich, T.; Blood-Forsythe, M.; Rappoport, D.; Kim, D.; Aspuru-Guzik, A. Calibration of the many-body dispersion range-separation parameter. , arXiv:1605.04987.
- Jasrasaria, D.; Pyzer-Knapp, E. O.; Rappoport, D.; Aspuru-Guzik, A. Space-filling curves as a novel crystal structure representation for machine learning models. , arXiv:1608.05747.
- Baghbanzadeh, M.; Bowers, C. M.; Rappoport, D.; Zaba, T.; Yuan, L.; Kang, K.; Liao, K.-C.; Gonidec, M.; Rothemund, P.; Cyganik, P.; Aspuru-Guzik, A.; Whitesides, G. M. Anomalously Rapid Tunneling: Charge Transport across SAMs of Oligoethylene Glycol. J. Am. Chem. Soc. , 139, 7624–7631.
- Parker, S. M.; Rappoport, D.; Furche, F. Quadratic Response Properties from TDDFT: Trials and Tribulations. J. Chem. Theory Comput. , 14, 807–819.
- Sawaya, N.; Rappoport, D.; Tabor, D. P.; Aspuru-Guzik, A. Excitonics: A Set of Gates for Molecular Exciton Processing and Signaling. ACS Nano , 21, 6410–6420.
- Cafferty, B. J.; Yuan L.; Baghbanzadeh, M.; Rappoport, D.; Beyzavi, M. H.; Whitesides; G. M. Charge Transport through Self‐Assembled Monolayers of Monoterpenoids. Angew. Chem. Int. Ed. , 58, 8097–8102.
- Rappoport, D. Reaction Networks and the Metric Structure of Chemical Space(s) J. Phys. Chem. A , 123, 2610–2620.
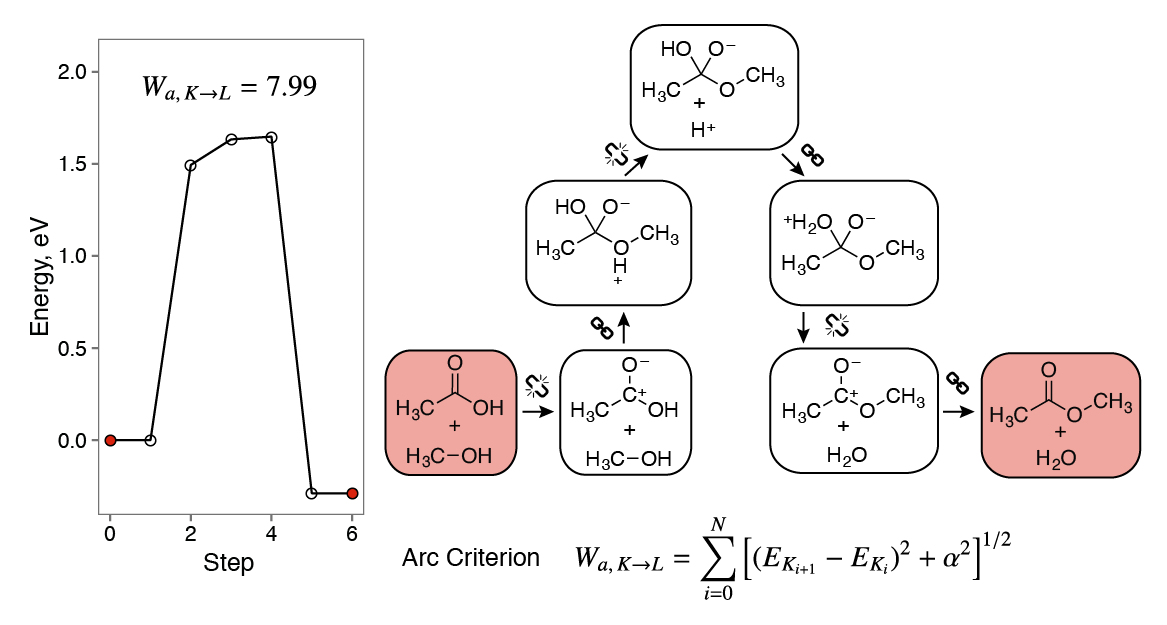
- Rappoport, D.; Aspuru-Guzik, A. Predicting Feasible Organic Reaction Pathways Using Heuristically Aided Quantum Chemistry J. Chem. Theory Comput. , 15, 4099–4112.
Scientific Presentations
- Practical aspects of molecular TDDFT calculations. 2nd International Workshop on TDDFT, , Benasque (Spain).
- Computational aspects of molecular TDDFT calculations. University of Illinois, , Urbana-Champaign, IL.
- Optimized Gaussian basis sets for linear and nonlinear response properties. 44th Symposium on Theoretical Chemistry, , Ramsau (Austria).
- TDDFT in chemistry and biochemistry III and IV. TDDFT Winter School, , Benasque (Spain).
- New approaches to analysis of resonant Raman spectra. 240th ACS National Meeting, , Boston, MA.
- Optimized basis sets and accuracy of electronic excitation energies in molecules. 242th ACS National Meeting, , Denver, CO.
- Prediction of coherent anti-stokes Raman (CARS) and surface-enhanced CARS spectra using density functional theory. 242th ACS National Meeting, , Denver, CO.
- Parametrized exciton dynamics in multichromophoric aggregates. 48th Symposium on Theoretical Chemistry, , Karlsruhe (Germany).
- New theoretical approaches to resonant and nonlinear Raman spectroscopies. Edgewood Chemical Biological Center, , Edgewood, MD.
- Construction and properties of prebiotic chemical reaction networks. 248th ACS National Meeting, , San Francisco, CA.
- Reaction networks. A simplification attempt. Advanced Methods for De Novo Prediction Of Chemical Reaction Networks Workshop, , Telluride, CO.
- Exploring reaction mechanisms with heuristics-aided quantum chemistry. 254th ACS National Meeting, , Washington, DC.